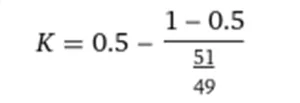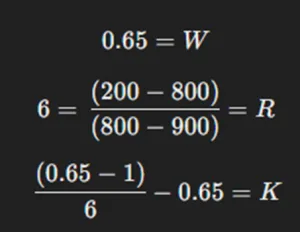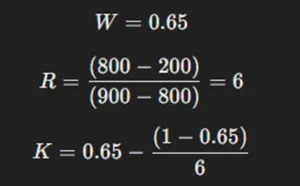روشهای جایگزین – معیارهای کلی
سایزبندی به روش Kelly یک روش محبوب در شرطبندی ورزشی سنتی است که برای تعیین سیستماتیک اندازه موقعیتها استفاده میشود. ممکن است منطق آن برای شما مشابه آنچه در آزمایش رالف وینس مشاهده شده است به نظر برسد، بنابراین ما کمی روند را تغییر میدهیم و با یک مثال شروع میکنیم:
بیایید یک بازی انجام دهیم—پرتاب سکهای که به نفع شما وزندار شده است:
- شیر: شما 51٪ مبلغ شرطبندی خود را برنده میشوید.
- خط: شما 49٪ مبلغ شرطبندی خود را از دست میدهید.
- شما با 1,000 دلار شروع میکنید.
چقدر شرط میبندید؟ آیا تمام 1,000 دلار را برای 10 بار پرتاب شرط میبندید؟ آیا 10 دلار را برای 1,000 بار پرتاب شرط میبندید؟ آیا این موضوع اهمیتی دارد؟
پاسخ شهودی این است که متوجه شوید شانس 51-49 به نفع شماست (EV مثبت است) و تمام پول خود را شرطبندی کنید. این یک معامله واضحاً نامتقارن است، اما این کار به خوبی پایان نخواهد یافت.
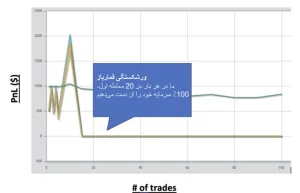
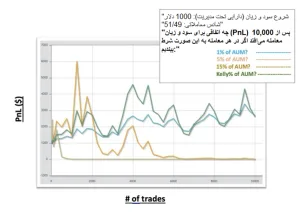
واضح است که ریسک کردن 100٪ از موجودی خود در هر بار پرتاب سکه، به طرز غیرمنطقیای تهاجمی است. اگر محافظهکارتر عمل کنید و 15٪ را به خطر بیندازید چه؟ 5٪ چطور؟
همانطور که مشاهده میکنید، وقتی 15٪ ریسک میکنید، احتمال ورشکستگی قبل از 1,000 معامله بسیار بالا است و وقتی 5٪ ریسک میکنید، این احتمال قبل از 6,000 معامله وجود دارد. به درس قبلی توجه کنید—شما باید زنده بمانید تا بتوانید از فرصت بهرهبرداری کنید. حالا که یک مثال را دیدید، بیایید ادامه دهیم.
ارزش مورد انتظار (Expected Value) را میتوان تقریباً به دو مؤلفه تقسیم کرد:
[A] تعداد دفعات معاملات برنده
[B] مقدار سود در هر معامله
معمولاً معاملات بهصورت یک بازی با مقدار کم برای [A] و مقدار بالا برای [B] هستند.
مثال:
به یک سری شرطبندیها از مثال خودمان نگاه کنیم. بعد از دو پرتاب، 4 نتیجه ممکن وجود دارد اما فقط 1 نتیجه برنده است:
- شیر & شیر: 1.51×1.51=2.281.51 \times 1.51 = 2.281.51×1.51=2.28 (+128%)
- شیر & خط: 1.51×0.51=0.771.51 \times 0.51 = 0.771.51×0.51=0.77 (-23%)
- خط & شیر: 0.51×1.51=0.770.51 \times 1.51 = 0.770.51×1.51=0.77 (-23%)
- خط & خط: 0.51×0.51=0.260.51 \times 0.51 = 0.260.51×0.51=0.26 (-74%)
بعد از 8 پرتاب، فقط سه نتیجه ممکن برنده هستند. بعداً بررسی میکنیم که چرا نتایج “خنثی” در واقع بازنده هستند، اما نکته مهم این است که بیشتر نتایج بازنده هستند.
برای هر معامله، یک اندازه بهینه برای معامله وجود دارد (بهعنوان درصدی از پرتفوی شما)—K%K\%K% در فرمول بالا. این مقدار، بازده مورد انتظار را در معاملات مکرر با ریسک مشابه به حداکثر میرساند. چگونه میتوانیم این فرمول را در بازی خود اعمال کنیم؟
- W=0.5W = 0.5W=0.5 (احتمال مساوی برای شیر و خط)
- R=51/49R = 51 / 49R=51/49
بنابراین، KKK تقریباً برابر است با 1.96٪
عالیه، اما چگونه میتوانیم این را در یک معامله واقعی اعمال کنیم؟
بیایید این را در یک معامله واقعی اعمال کنیم:
ما قصد نداریم وارد تمام جزئیات تنظیم معامله شویم، اما این یک محیط مناسب برای یک موقعیت شورت روزانه در MOVE بود. فرض کنید که ما تمام معاملات را ثبت کردهایم و زمانی که MOVE را شورت میکنیم، نرخ برد 65٪ داریم و نسبت پاداش به ریسک 6 به 1 (نتیجه متوسط 6R بهصورت سنتی) است.
MOVE برخلاف فیوچرز دائمی سنتی رفتار میکند، اما میتوانید بهراحتی چیزی مانند ETH را جایگزین کنید—چیزی که مهم است این است که شما داشته باشید:
- قیمتهای هدف برای گرفتن سود و استاپلاس
- یک توزیع تقریبی احتمالاتی از نتایج در ذهن (به همین دلیل ثبت معاملات مهم است)
حالا به معامله “مثال” برگردیم:
- MOVE روزانهای که قصد شورت کردن آن را داشتم در حدود 800 دلار باز شد.
- معتقد بودم 65٪ احتمال وجود دارد که قیمت به 200 دلار کاهش یابد.
- معتقد بودم 35٪ احتمال وجود دارد که قیمت به 900 دلار افزایش یابد و استاپ من فعال شود.
- برای سادگی فرض میکنیم این دو تنها نتایج ممکن هستند.
حالا به فرمول K% برگردیم:
بنابراین، اندازه بهینه نظری شرط من برای این معامله، تقریباً 59.16٪ از پرتفوی من بود.
با این حال، این مقدار برای من بیش از حد تهاجمی است، بنابراین به احتمال زیاد اندازه نصف کلی را در نظر میگیرم و حدوداً 30٪ اختصاص میدهم.
پس معامله چگونه پیش رفت؟
MOVE روزانهای که قصد شورت کردن آن را داشتم، حدود 800 دلار باز شد.
معتقد بودم 65٪ احتمال وجود دارد که قیمت به 200 دلار کاهش پیدا کند.
معتقد بودم 35٪ احتمال وجود دارد که قیمت به 900 دلار افزایش پیدا کند و استاپلاس من فعال شود.
برای سادگی فرض میکنیم که این دو تنها نتایج ممکن هستند.
حالا دوباره به فرمول K% برگردیم:
اندازه بهینه نظری شرط من برای این معامله، تقریباً 59.16٪ از پرتفوی من بود.
با این حال، این مقدار برای من بیش از حد تهاجمی است، بنابراین به احتمال زیاد اندازه نصف کلی (Half-Kelly) را در نظر میگیرم و تقریباً 30٪ از پرتفوی را اختصاص میدهم.
پس نتیجه این معامله چه شد؟
استفاده از Kelly Sizing گاهی میتواند نسبت به روشهای سادهتر تهاجمیتر باشد، اما این روش به شما اجازه میدهد تا با واقعیت سازگار شوید که همه معاملات یکسان نیستند. زمانی که برتری (Edge) وجود دارد و شرایط به نفع شماست، گاهی اوقات بهینه است که از این برتری استفاده بیشتری کنید.
حالا، واقعبینانه نگاه کنیم—نتایج معاملات دو حالتی (Nonbinary) نیستند. توزیعهای احتمالی در دنیای واقعی پیوسته (Continuous) هستند—نه گسسته (Discrete). خوشبختانه، اد تورپ (Ed Thorp) با ارائه نسخه اصلاحشدهای از روش Kelly، راهحلی برای این موضوع پیدا کرد. به طور خلاصه:
- حرکات یک سکه را به N (∞) رویداد دو حالتی تقسیم کنید.
- Kelly را روی هر کدام اعمال کنید.
- انتگرالگیری (Integrate) انجام دهید.